How does lmer (from the R package lme4) compute lo

I'm trying to understand the function lmer. I've found plenty of information about how to use the command, but not much about what it's actually doing (save for some cryptic comments here: http://www.bioconductor.org/help/course-materials/2008/PHSIntro/lme4Intro-handout-6.pdf). I'm playing with the following simple example:

library(data.table)
library(lme4)
options(digits=15)

n<-1000
m<-100
data<-data.table(id=sample(1:m,n,replace=T),key="id")
b<-rnorm(m)
data$y<-rand[data$id]+rnorm(n)*0.1
fitted<-lmer(b~(1|id),data=data,verbose=T)
fitted

I understand that lmer is fitting a model of the form Y_{ij} = beta + B_i + epsilon_{ij}, where epsilon_{ij} and B_i are independent normals with variances sigma^2 and tau^2 respectively. If theta = tau/sigma is fixed, I computed the estimate for beta with the correct mean and minimum variance to be

c = sum_{i,j} alpha_i y_{ij}

where

alpha_i = lambda/(1 + theta^2 n_i)
lambda = 1/[\sum_i n_i/(1+theta^2 n_i)]
n_i = number of observations from group i

~~I also computed the following unbiased estimate for sigma^2:~~

~~s^2 = \sum_{i,j} alpha_i (y_{ij} - c)^2 / (1 + theta^2 - lambda)~~

These estimates seem to agree with what lmer produces. However, I can't figure out how log likelihood is defined in this context. I calculated the probability density to be

pd(Y_{ij}=y_{ij}) = \prod_{i,j}[f_sigma(y_{ij}-ybar_i)]
    * prod_i[f_{sqrt(sigma^2/n_i+tau^2)}(ybar_i-beta) sigma sqrt(2 pi/n_i)]

where

ybar_i = \sum_j y_{ij}/n_i (the mean of observations in group i)
f_sigma(x) = 1/(sqrt{2 pi}sigma) exp(-x^2/(2 sigma)) (normal density with sd sigma)

But log of the above is not what lmer produces. How is log likelihood computed in this case (and for bonus marks, why)?

Edit: Changed notation for consistency, striked out incorrect formula for standard deviation estimate.

标签： r lmer random-effects

1条回答

Evening l夕情丶

2楼-- · 2019-03-13 11:36

The links in the comments contained the answer. Below I've put what the formulae simplify to in this simple example, since the results are somewhat intuitive.

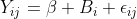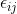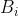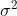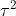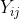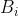lmer fits a model of the form $Y_{ij} = \beta + B_i + \epsilon_{ij}$ , where $\epsilon_{ij}$ and $B_i$ are independent normals with variances $\sigma^2$ and $\tau^2$ respectively. The joint probability distribution of $Y_{ij}$ and $B_i$ is therefore

$\left(\prod_{i,j}f_{\sigma^2}(y_{ij}-\beta-b_i)\right)\left(\prod_i f_{\tau^2}(b_i)\right)$

where

$f_{\sigma^2}(x)=\frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{x^2}{2\sigma^2}}$ .

The likelihood is obtained by integrating this with respect to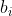 $b_i$ (which isn't observed) to give

$\left(\prod_{i,j}f_{\sigma^2}(y_{ij}-\bar y_i)\right)\left(\prod_i f_{\sigma^2/n_i+\tau^2}(\bar y_i-\beta)\sqrt{2\pi\sigma^2/n_i}\right)$

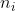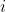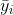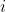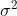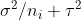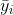where $n_i$ is the number of observations from group $i$ , and $\bar y_i$ is the mean of observations from group $i$ . This is somewhat intuitive since the first term captures spread within each group, which should have variance $\sigma^2$ , and the second captures the spread between groups. Note that $\sigma^2/n_i+\tau^2$ is the variance of $\bar y_i$ .

However, by default (REML=T) lmer maximises not the likelihood but the "REML criterion", obtained by additionally integrating this with respect to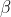 $\beta$ to give

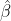$\left(\prod_{i,j}f_{\sigma^2}(y_{ij}-\bar y_i)\right)\left(\prod_i f_{\sigma^2/n_i+\tau^2}(\bar y_i-\hat\beta)\sqrt{2\pi\sigma^2/n_i}\right)\sqrt{\frac{2\pi\sigma^2}{\sum_i\frac{n_i}{1+n_i\theta^2}}}$

where $\hat\beta$ is given below.

Maximising likelihood (REML=F)

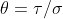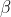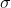If $\theta=\tau/\sigma$ is fixed, we can explicitly find the $\beta$ and $\sigma$ which maximise likelihood. They turn out to be

$\hat\beta=\frac{\sum_{i,j}y_{ij}/(1+n_i\theta^2)}{\sum_i n_i/(1+n_i\theta^2)}$

$\hat\sigma^2=\frac{1}{n}\left(\sum_{i,j}(y_{ij}-\bar y_i)^2+\sum_i\frac{n_i}{1+n_i\theta^2}(\bar y_i-\hat\beta)^2\right)$

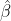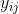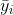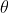Note $\hat\sigma^2$ has two terms for variation within and between groups, and $\hat\beta$ is somewhere between the mean of $y_{ij}$ and the mean of $\bar y_i$ depending on the value of $\theta$ .

Substituting these into likelihood, we can express the log likelihood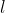 $l$ in terms of 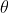$\theta$ only:

$-2l=\sum_i\log(1+n_i\theta^2)+n(1+\log(2\pi\hat\sigma^2))$

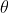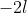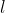lmer iterates to find the value of $\theta$ which minimises this. In the output, $-2l$ and $l$ are shown in the fields "deviance" and "logLik" (if REML=F) respectively.

Maximising restricted likelihood (REML=T)

Since the REML criterion doesn't depend on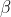 $\beta$ , we use the same estimate for 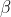$\beta$ as above. We estimate 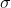$\sigma$ to maximise the REML criterion:

$\hat\beta=\frac{\sum_{i,j}y_{ij}/(1+n_i\theta^2)}{\sum_i n_i/(1+n_i\theta^2)}$

$\hat\sigma^2=\frac{1}{n-1}\left(\sum_{i,j}(y_{ij}-\bar y_i)^2+\sum_i\frac{n_i}{1+n_i\theta^2}(\bar y_i-\hat\beta)^2\right)$

The restricted log likelihood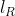 $l_R$ is given by

$-2l_R=\sum_i\log(1+n_i\theta^2)+(n-1)(1+\log(2\pi\hat\sigma^2))+\log\left(\sum_i\frac{n_i}{1+n_i\theta^2}\right)$

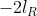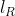In the output of lmer, $-2l_R$ and $l_R$ are shown in the fields "REMLdev" and "logLik" (if REML=T) respectively.

0人赞添加讨论(0) 举报