In-order tree traversal

Question

I have the following text from an academic course I took a while ago about in-order traversal (they also call it pancaking) of a binary tree (not BST):

In-order tree traversal

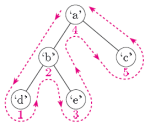
Draw a line around the outside of the tree. Start to the left of the root, and go around the outside of the tree, to end up to the right of the root. Stay as close to the tree as possible, but do not cross the tree. (Think of the tree — its branches and nodes — as a solid barrier.) The order of the nodes is the order in which this line passes underneath them. If you are unsure as to when you go “underneath” a node, remember that a node “to the left” always comes first.

Here's the example used (slightly different tree from below)

However when I do a search on google, I get a conflicting definition. For example the wikipedia example:

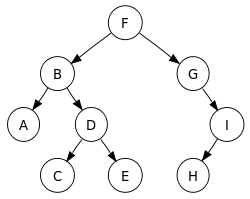
Inorder traversal sequence: A, B, C, D, E, F, G, H, I (leftchild,rootnode,right node)

But according to (my understanding of) definition #1, this should be

A, B, D, C, E, F, G, I, H

Can anyone clarify which definition is correct? They might be both describing different traversal methods, but happen to be using the same name. I'm having trouble believing the peer-reviewed academic text is wrong, but can't be certain.

Answer 1

In my bad attempt at the drawing here's the order that shows how they should be picked.

pretty much pick the node that is directly above the line being drawn,.

Answer 2

I think the first binary tree with the root of a is a Binary tree which is not correctly constructed.

Try to implement so that all the left side of the tree is less than the root and all the right side of the tree is greater than or equal to the root.

Answer 3

It is correct for preorder,nt for inorder

Answer 4

void
inorder (NODE root)
{
  if (root != NULL)
    {
      inorder (root->llink);
      printf ("%d\t", root->info);
      inorder (root->rlink);
    }
}

This the most simplest approach to recursive definition of in-order traversal, just call this function in the main function to get the in-order traversal of a given binary tree.

Answer 5

Both definitions give the same result. Don't be fooled by the letters in the first example - look at the numbers along the path. The second example does use letters to denote the path - perhaps that is what is throwing you off.

For example, in your example order showing how you thought the second tree would be traversed using the algorithm of the first one, you place "D" after "B" but you shouldn't because there is still a left-hand child node of D available (that's why the first item says "the order in which this line passes underneath them."

Answer 6

The proper traversal would be: as far left as possible with leaf nodes (not root nodes)

Left Root Right

A B NULL

C D E

Null F G

H I NULL

F is root or left, i am not sure