Efficient comparison of 100.000 vectors

Question

I save 100.000 Vectors of in a database. Each vector has a dimension 60. (int vector[60])

Then I take one and want present vectors to the user in order of decreasing similarity to the chosen one.

I use Tanimoto Classifier to compare 2 vectors:

Is there any methods to avoid doing through all entries in the database?

One more thing! I don't need to sort all vectors in the database. I whant to get top 20 the most similar vectors. So maybe we can roughly threshold 60% of entries and use the rest for sorting. What do you think?

Answer 1

In short, no, probably not any way to avoid going through all the entries in the database. One qualifier on that; if you have a significant number of repeated vectors, you may be able to avoid reprocessing exact repeats.

Answer 2

In order to sort something, you need a sorting key for each item. So you will need to process each entry at least once to calculate the key.

Is that what you think of?

======= Moved comment here:

Given the description you cannot avoid looking at all entries to calculate your similarity factor. If you tell the database to use the similarity factor in the "order by" clause you can let it do all the hard work. Are you familiar with SQL?

Answer 3

Another take on this is the all pair problem with a given threshold for some similarity function. Have a look at bayardo's paper and code here http://code.google.com/p/google-all-pairs-similarity-search/

I do not know if your similarity function matches the approach, but if so, that is another tack to look at. It would also require normalized and sorted vectors in any case.

Answer 4

Uh, no?

You only have to do all 99,999 against the one you picked (rather than all n(n-1)/2 possible pairs), of course, but that's as low as it goes.

---

Looking at your response to nsanders's answer, it is clear you are already on top of this part. But I've thought of a special case where computing the full set of comparisons might be a win. If:

• the list comes in slowly (say your getting them from some data acquisition system at a fixed, low rate)
• you don't know until the end which one you want to compare to
• you have plenty of storage
• you need the answer fast when you do pick one (and the naive approach isn't fast enough)
• Looks are faster than computing

then you could pre-compute the as the data comes in and just lookup the results per pair at sort time. This might also be effective if you will end up doing many sorts...

Answer 5

Newer answer

How much preprocessing can you do? Can you build "neighborhoods" ahead of time and note which neighborhood each vector is in inside the database? That might let you eliminate many vectors from consideration.

---

Old answer below, which assumed 60 was magnitude of all the vectors, not the dimension.

Since the vectors are all the same length (60), I think you're doing too much math. Can't you just do the dot product of the chosen one against each candidate?

In 3D: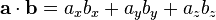

Three multiplies. In 2D it's just two multiplies.

Or does that violate your idea of similarity? To me, the most similar vectors are the ones with the least angular distance between them.

Answer 6

If you're willing to live with approximations, there are a few ways you can avoid having to go through the whole database at runtime. In a background job you can start pre-computing pairwise distances between vectors. Doing this for the whole database is a huge computation, but it does not need to be finished for it to be useful (i.e. start computing distances to 100 random vectors for each vector or so. store results in a database).

Then triangulate. if the distance d between your target vector v and some vector v' is large, then the distance between v and all other v'' that are close to v' will be large(-ish) too, so there is no need to compare them anymore (you will have to find acceptable definitions of "large" yourself though). You can experiment with repeating the process for the discarded vectors v'' too, and test how much runtime computation you can avoid before the accuracy starts to drop. (make a test set of "correct" results for comparisons)

good luck.

sds