Can anyone provide some pseudo code for a roulette selection function? How would I implement this:
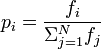
I don't really understand how to read this math notation. I never took any probability or statistics.
Can anyone provide some pseudo code for a roulette selection function? How would I implement this:
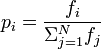
I don't really understand how to read this math notation. I never took any probability or statistics.
This Swift 4 array extension implements weighted random selection, a.k.a Roulette selection from its elements:
For example given the two element array:
weightedRandomIndex()will return zero 90% of the time and one 10% of the time.Here is a more complete test:
output:
This answer is basically the same as Andrew Mao's answer here: https://stackoverflow.com/a/15582983/74975
It's been a few years since i've done this myself, however the following pseudo code was found easily enough on google.
for all members of population sum += fitness of this individual end for for all members of population probability = sum of probabilities + (fitness / sum) sum of probabilities += probability end for loop until new population is full do this twice number = Random between 0 and 1 for all members of population if number > probability but less than next probability then you have been selected end for end create offspring end loopThe site where this came from can be found here if you need further details.
Roulette Wheel Selection in MatLab:
Here is some code in C :
Here's a compact java implementation I wrote recently for roulette selection, hopefully of use.
From the above answer, I got the following, which was clearer to me than the answer itself.
To give an example:
Random(sum) :: Random(12) Iterating through the population, we check the following: random < sum
Let us chose 7 as the random number.
Through this example, the most fit (Index 3) has the highest percentage of being chosen (33%); as the random number only has to land within 6->10, and it will be chosen.