Affinity Propagation preferences initialization

问题:

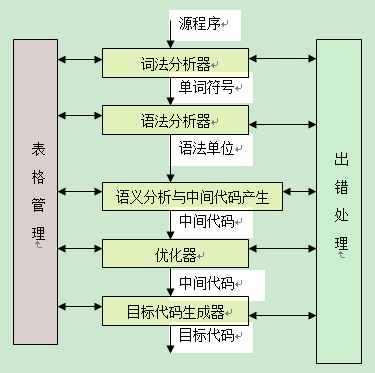
I need to perform clustering without knowing in advance the number of clusters. The number of cluster may be from 1 to 5, since I may find cases where all the samples belong to the same instance, or to a limited number of group. I thought affinity propagation could be my choice, since I could control the number of clusters by setting the preference parameter. However, if I have a single cluster artificially generated and I set preference to the minimal euclidean distance among nodes (to minimize number of clusters), I get terrible over clustering.

"""
=================================================
Demo of affinity propagation clustering algorithm
=================================================

Reference:
Brendan J. Frey and Delbert Dueck, "Clustering by Passing Messages
Between Data Points", Science Feb. 2007

"""
print(__doc__)
import numpy as np
from sklearn.cluster import AffinityPropagation
from sklearn import metrics
from sklearn.datasets.samples_generator import make_blobs
from scipy.spatial.distance import pdist

##############################################################################
# Generate sample data
centers = [[0,0],[1,1]]
X, labels_true = make_blobs(n_samples=300, centers=centers, cluster_std=0.5,
                            random_state=0)
init = np.min(pdist(X))

##############################################################################
# Compute Affinity Propagation
af = AffinityPropagation(preference=init).fit(X)
cluster_centers_indices = af.cluster_centers_indices_
labels = af.labels_

n_clusters_ = len(cluster_centers_indices)

print('Estimated number of clusters: %d' % n_clusters_)
print("Homogeneity: %0.3f" % metrics.homogeneity_score(labels_true, labels))
print("Completeness: %0.3f" % metrics.completeness_score(labels_true, labels))
print("V-measure: %0.3f" % metrics.v_measure_score(labels_true, labels))
print("Adjusted Rand Index: %0.3f"
      % metrics.adjusted_rand_score(labels_true, labels))
print("Adjusted Mutual Information: %0.3f"
      % metrics.adjusted_mutual_info_score(labels_true, labels))
print("Silhouette Coefficient: %0.3f"
      % metrics.silhouette_score(X, labels, metric='sqeuclidean'))

##############################################################################
# Plot result
import matplotlib.pyplot as plt
from itertools import cycle

plt.close('all')
plt.figure(1)
plt.clf()

colors = cycle('bgrcmykbgrcmykbgrcmykbgrcmyk')
for k, col in zip(range(n_clusters_), colors):
    class_members = labels == k
    cluster_center = X[cluster_centers_indices[k]]
    plt.plot(X[class_members, 0], X[class_members, 1], col + '.')
    plt.plot(cluster_center[0], cluster_center[1], 'o', markerfacecolor=col,
             markeredgecolor='k', markersize=14)
    for x in X[class_members]:
        plt.plot([cluster_center[0], x[0]], [cluster_center[1], x[1]], col)

plt.title('Estimated number of clusters: %d' % n_clusters_)
plt.show()

Is there any flaw in my approach of using Affinity Propagation? Conversely, is Affinity Propagation unsuited for this task, so should I use something else?

回答1:

No, there is no flaw. AP does not use distances, but requires you to specify a similarity. I don't know the scikit implementation so well, but according to what I read, it uses negative squared Euclidean distances by default to compute the similarity matrix. If you set the input preference to the minimal Euclidean distance, you get a positive value, while all similarities are negative. So this will typically result in as many clusters as you have samples (note: the higher the input preference, the more clusters). I'd rather suggest to set the input preference to the minimal negative squared distance, i.e. -1 times the square of the largest distance in the data set. This will give you a much smaller number of clusters, but not necessarily one single cluster. I don't know whether the preferenceRange() function exists also in the scikit implementation. There is Matlab code on the AP homepage and it is also implemented in the R package 'apcluster' that I am maintaining. This function allows for determining meaningful bounds for the input preference parameter. I hope that helps.

回答2:

You can control it by specifying the minimum preferences, but it's not sure that you will found a single cluster.

And also, I would suggest you to don't wanna make a single cluster because it would generate errors, as some data must not be the same or have similarity with examplers but as you provide the minimum preferences so the AP will commit the error.