I've got a problem concerning combinatorics. Unfortunately, I can't describe it abstractly so I try to explain it as a story. :)
Problem:
- There are 100 children on the schoolyard.
- They all have unique heights, assuming the values are 100-199cm.
- You want to build 10 groups, each consisting of 1-99 children.
- How can you build all the groups while the children must be sorted by their height?
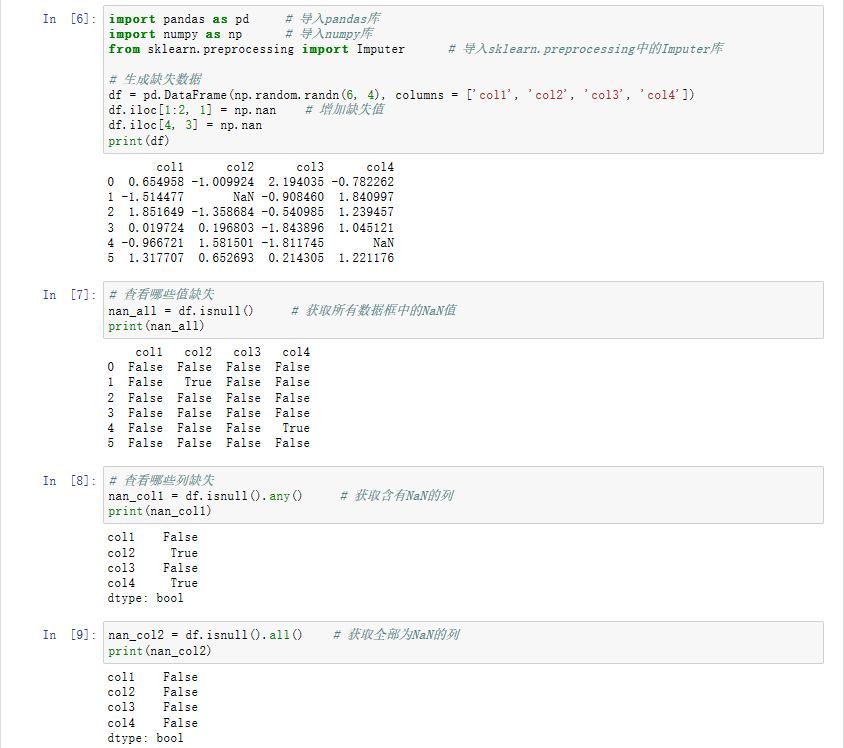
- I need all possible solutions for these groups since it isn't hard to find one constellation.
Short and easy:
All 100 children stand side by side. You only have to decide where to split them into groups and find all solutions for this.
Example (values are the heights):
[120 ... 190 ... 199] ... [126 ... 137 ... 144 ... 188] is not possible
[101] ... [104 ... 105 ... 112 ... 149] ... [169 ... 189] is possible
I hope you can help me. Thank you very much in advance!
PS: It's no homework. ;) Normally, I need a function which does this with numbers. But I couldn't describe this abstractly like "building k groups of numbers while all numbers are sorted". I thought you wouldn't understand it this way. :) A solution in PHP would be best but I would be glad to see solutions in other languages as well. :)
As I understand it, you are effectively asking for ways of partitioning the interval [100,199] into 10 parts, i.e. you want to find numbers x[0], ..., x[10] such that:
x[0] = 100 < x[1] < x[2] < ... < x[9] < x[10] = 199
Define a recursive function partition(intervalSize, pieces) which counts the number of ways to partition a given interval. You are after partition(100, 10).
The following Java code counts the partitions (sorry, don't know PHP that well):
public class Partitions
{
static long[][] partitions = new long[100][10];
private static long partition(int intervalSize, int pieces)
{
if (partitions[intervalSize-1][pieces-1] != 0) {
return partitions[intervalSize-1][pieces-1];
}
long partition = 0L;
if (pieces == 1) {
partition = 1L;
} else {
for (int i = 1; i <= intervalSize - 1; i++) {
partition += partition(intervalSize - i, pieces - 1);
}
}
partitions[intervalSize-1][pieces-1] = partition;
return partition;
}
public static void main(String[] args)
{
System.out.println(partition(100, 10));
}
}
The following Java code prints out the actual partitions. Because the number of partitions is so high for (100,10), I'm illustrating the answer for (5,3):
public class Partitions2
{
private static void showPartitions(int sizeSet, int numPartitions)
{
showPartitions("", 0, sizeSet, numPartitions);
}
private static void showPartitions(String prefix, int start, int finish,
int numLeft)
{
if (numLeft == 0 && start == finish) {
System.out.println(prefix);
} else {
prefix += "|";
for (int i = start + 1; i <= finish; i++) {
prefix += i + ",";
showPartitions(prefix, i, finish, numLeft - 1);
}
}
}
public static void main(String[] args)
{
showPartitions(5, 3);
}
}
The output is:
|1,|2,|3,4,5,
|1,|2,3,|4,5,
|1,|2,3,4,|5,
|1,2,|3,|4,5,
|1,2,|3,4,|5,
|1,2,3,|4,|5,
I need all possible solutions for
these groups since it isn't hard to
find one constellation.
Normally, there 100! ways to permute 100 items, but since you're preserving order, you can reduce your problem size down substantially. What you're describing is an integer partitioning problem. For example, let's say you were partitioning the number 5 into all possible integer subsets which add up to 5, you'd get the sets {5}, {4, 1}, {3, 2}, {3, 1, 1,}, {2, 2, 1}, {2, 1, 1, 1}, {1, 1, 1, 1, 1}.
The number of integer partitions grows exponentially with the size of the integer, but the exponential growth is slow enough that you can enumerate through all partitions of n = 100, since there are only 190,569,292 of them. The additional constraint here is that you want to filter all of your partitions for sets containing exactly 10 items, which is easy to enumerate through using a Ferrer diagram.
I can demonstrate a Ferrer diagram by partition the number 20 into 3 buckets: start with a 20 col x 3 row grid as follows:
12345678901234567890
1******************
2*
3*
So, the first partition is {18, 1, 1}
Now move an item from the top of the stack into the next slot:
12345678901234567890
1*****************
2**
3*
Our new partition is {17, 2, 1}. We can another item from one stack to the other:
12345678901234567890
1****************
2***
3*
Now we have {16, 3, 1}. You continue in this fashion until you've enumerate all permutations (its up to you whether {17, 1, 2} is a distinct partition from {17, 2, 1}).
From this point, you should be able to envision the general outline of the algorithm you need -- that is, if you'd like the challenge of writing this function from scratch. Other people have already written lots of efficient functions to solve the problem easily.


![Prime Path[POJ3126] [SPFA/BFS] Prime Path[POJ3126] [SPFA/BFS]](https://oscimg.oschina.net/oscnet/e1200f32e838bf1d387d671dc8e6894c37d.jpg)
