Finding out if a point is inside a voronoi cell

问题:

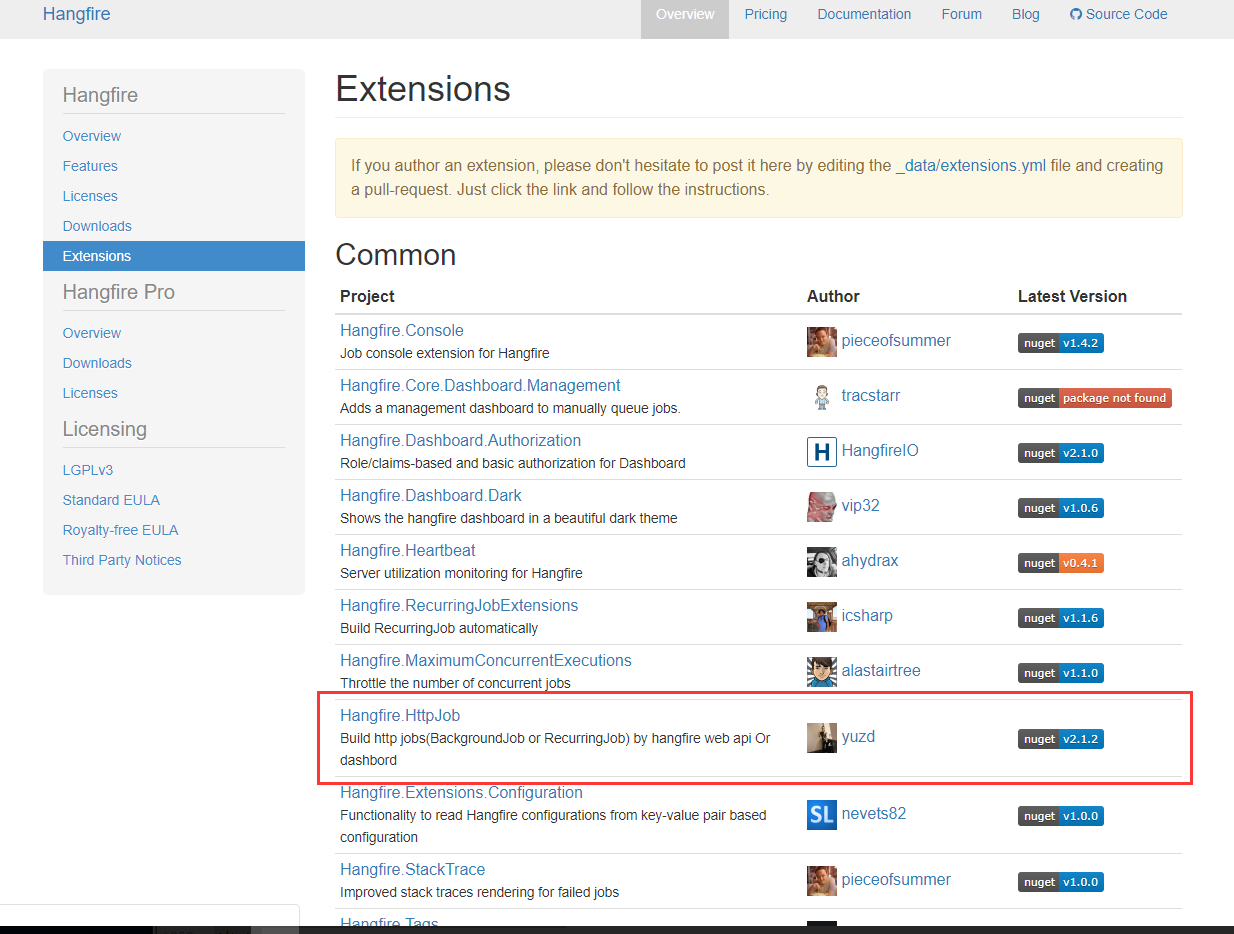
Is there a simple way to find out if a point is inside a voronoi cell?

For example, the following code generates something like the diagram below:

using namespace boost::polygon;

point_data<int> p1(0, 0);
point_data<int> p2(-10, 10);
point_data<int> p3(-10, -10);
point_data<int> p4(10, -10);
point_data<int> p5(10, 10);

std::vector<point_data<int>> pts = { p1, p2, p3, p4, p5 };
construct_voronoi(pts.begin(), pts.end(), vd);

In this case, how can I found out if the point (5,5) is inside the central cell?

I could create a polygon out of each cell and find out using a point in polygon algorithm, but I'm interested in knowing the library offers something "for free".

回答1:

Like, @Magnus Hoff commented, the cell defined by the closest center to your query point must contain it (up to distance ties). In fact, this is from the definition of a Voronoii cell, i.e. the point set whose members are closer to the cell center than to any other centers. So, this query really doesn't require boost::polygon or the half-line algorithm:

//using namespace boost::polygon;
using namespace std;
#include <iostream>
#include <vector>
#include <limits>

template <typename T> 
using point_data = std::pair<T,T>;
point_data<int> p1(0, 0);
point_data<int> p2(-10, 10);
point_data<int> p3(-10, -10);
point_data<int> p4(10, -10);
point_data<int> p5(10, 10);

std::vector<point_data<int>> pts = { p1, p2, p3, p4, p5 };
//construct_voronoi(pts.begin(), pts.end(), vd);


double dist2(point_data<int> pt1,point_data<int> pt2) {
  return (pt1.first-pt2.first)*(pt1.first-pt2.first) + (pt1.first-pt2.second)* (pt1.first-pt2.second);
}

bool isInCell(point_data<int> point) {
  double d = numeric_limits<double>::max();

  point_data<int> ptClose;
  for (auto& pt:pts) {
    if (dist2(pt,point) < d)
      ptClose = pt;
  }
  return ptClose == point;
}

int main() {
  cout << isInCell(make_pair(5,5)) << endl;
}

回答2:

You want point location test, especially a kirkpatrick data structure for point location test but it is a little bit complicated. Instead you can give each voronoi cell a color and check the color at the point.