Adding L1/L2 regularization in PyTorch?

问题:

Is there any way, I can add simple L1/L2 regularization in PyTorch? We can probably compute the regularized loss by simply adding the data_loss with the reg_loss but is there any explicit way, any support from PyTorch library to do it more easily without doing it manually?

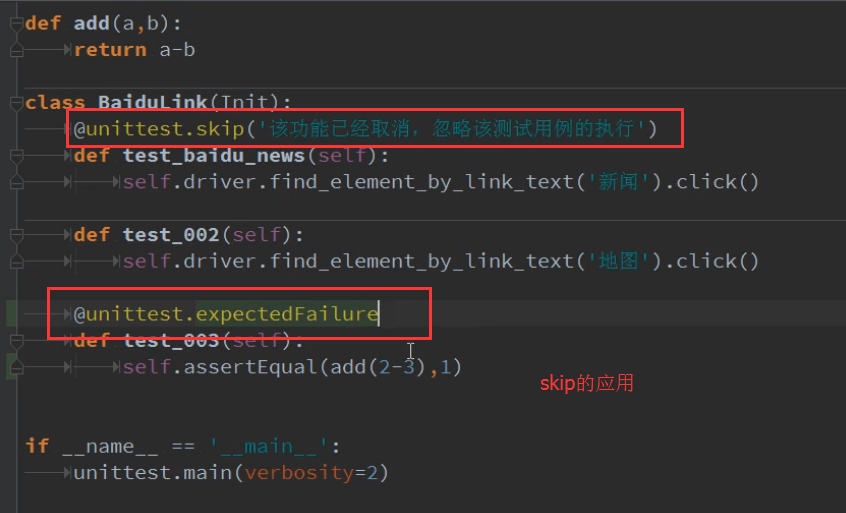
回答1:

This is presented in the documentation for PyTorch. Have a look at http://pytorch.org/docs/optim.html#torch.optim.Adagrad. You can add L2 loss using the weight decay parameter to the Optimization function.

回答2:

Following should help for L2 regularization:

optimizer = torch.optim.Adam(model.parameters(), lr=1e-4, weight_decay=1e-5)

回答3:

For L2 regularization,

lambda = torch.tensor(1.)
l2_reg = torch.tensor(0.)
for param in model.parameters():
    l2_reg += torch.norm(param)
loss += lambda * l2_reg

References:

• https://discuss.pytorch.org/t/how-does-one-implement-weight-regularization-l1-or-l2-manually-without-optimum/7951.
• http://pytorch.org/docs/master/torch.html?highlight=norm#torch.norm.

回答4:

Interesting torch.norm is slower on CPU and faster on GPU vs. direct approach.

import torch
x = torch.randn(1024,100)
y = torch.randn(1024,100)

%timeit torch.sqrt((x - y).pow(2).sum(1))
%timeit torch.norm(x - y, 2, 1)

Out:

1000 loops, best of 3: 910 µs per loop
1000 loops, best of 3: 1.76 ms per loop

On the other hand:

import torch
x = torch.randn(1024,100).cuda()
y = torch.randn(1024,100).cuda()

%timeit torch.sqrt((x - y).pow(2).sum(1))
%timeit torch.norm(x - y, 2, 1)

Out:

10000 loops, best of 3: 50 µs per loop
10000 loops, best of 3: 26 µs per loop

回答5:

for L1 regularization and inclulde weight only:

L1_reg = torch.tensor(0., requires_grad=True)
for name, param in model.named_parameters():
    if 'weight' in name:
        L1_reg = L1_reg + torch.norm(param, 1)

total_loss = total_loss + 10e-4 * L1_reg