两条线之间的角度开始于线的一侧(Angle between two lines beginning

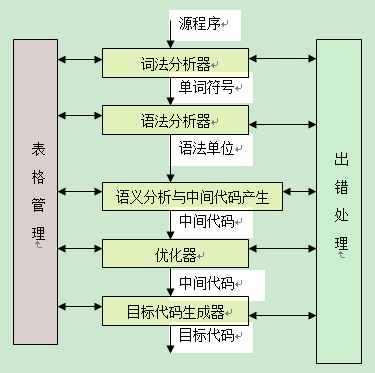
我有X两点指定两行和y坐标的每个。第一个点（在线条开始）是，我有3点A，B和C，其中一个线是从A到B并从A到C.我会然后把要计算两个之间的角度的另一个等于含义开始在第一行的右侧线。结果不必是精确的I实际上只需要知道，如果此角度大于或小于 180°（π弧度）。感谢您的帮助 - 你不需要编写任何代码，伪代码和/或解释将是巨大的。

Answer 1:

让我们来定义一些符号：

A := (a1, a1).
B := (b1, b2).
C := (c1, c2).

然后，矩阵的行列式d

1 a1 a2
1 b1 b2
1 c1 c2

确定是否C位于左侧或右侧的引导线的AB [比照计算几何 - 伯格，面包车Kreveld，奥维马斯，施华蔻 - 第1章习题1.4）]

现在，你可以从行2和3减去第1行：

1 a1     a2
0 b1-a1 b2-a2
0 c1-a1 c2-a2

并计算D从第一列获得：

(b1-a1)*(c2-a2) > (c1-a1)*(b2-a2)

作为表示是否满足条件C位于左侧AC与否。当然，躺在右侧（相应的左侧）表示的角度是<180（分别地，> 180）

例

A = (0, 0)
B = (0, 1)
C = (1, 0)

然后AB是垂直段（y轴）和C显然是在其右侧。条件

(b1-a1)*(c2-a2) > (c1-a1)*(b2-a2)           ineq(1)

变为：

0 > 1

这是false的，这意味着C不上的左侧AB （如预期）

可视化

以可视化的条件下，我们可以翻译三点A ， B和C直到A变(0,0) 这是一种无害的变换，因为（1）在ineq条件减去a1和a2从坐标B和C 。有了这个翻译ineq（1）变为：

b1*c2 > c1*b2                              ineq(2)

现在，让我们想象的三个点（忽略现在相对于棕色系C' = (c'1, c'2)

该产品b1*c2是红色矩形的面积。该产品c1*b2是绿色矩形的面积。图为RED <GREEN意味着C是在右边。

现在，精神上移动C身边，说C'和可视化的新的红色和绿色的矩形。不平等只要保持有效C是在右边。

还不相信？好了，写一个程序，而你改变的立场，即动态地再现了这张照片C ，瞧！（或学习一些数学和解决本书的锻炼;）

注：请注意，这些矩形有一个标志。在图片中他们都有一个积极的区域，然而，在一般情况下，产品b1*c2和b2*c1将有一个标志。

Answer 2:

看看的向量积。如果计算线段AB和AC的3D矢量，他们都将是零个z分量。

由于矢量AB和AC趴在xy平面，其矢量产品的唯一可能的非零分量为Z分量 - 所以这是你需要计算的唯一部件。

此z分量的符号会告诉你的角度是否超过或者根据您的方位小于180度。