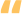矩形相交（垂直线）(Rectangles Intersection (Vertical line))

对于给定的矩形R1我试图找出哪些是可以用它相交如果我画一个vectical线段其他矩形。

与相交的矩形R1被标记为红色。

每个矩形的特征在于其(top, left)和(bottom, right)坐标。

R1 = [top, left, bottom, right],...,Rn = [top, left, bottom, right]

通过使用坐标和垂直线。 我想找到与R1相交的矩形

解

我发现下面的库，做同样的工作，正如ICL升压库，但必须简单：下载网站：[ https://github.com/ekg/intervaltree][2]

#include <iostream>
#include <fstream>
#include "IntervalTree.h"

using namespace std;

struct Position
{
    int x;
    int y;
    string id;
};

int main()
{
    vector<Interval<Position>> intervals;
    intervals.push_back(Interval<Position>(4,10,{1,2,"r1"}));
    intervals.push_back(Interval<Position>(6,10,{-6,-3,"r2"}));
    intervals.push_back(Interval<Position>(8,10,{5,6,"r3"}));

    vector<Interval<Position> > results;
    vector<string> value;
    int start = 4;
    int stop = 10;

    IntervalTree<Position> tree(intervals);
   // tree.findContained(start, stop, results);
    tree.findOverlapping(start, stop, results);
    cout << "found " << results.size() << " overlapping intervals" << endl;
}

---

例

• LEFT = 4;
• RIGHT = 10;
• 结构{1,2， “RC1”};

intervals.push_back（时间间隔（4,10，{1,2， “R1”}））;

Answer 1:

你不关心的矩形是垂直。 您可以投射到所有的X轴，然后解决相应的1维的问题：你有一个设定的时间间隔的，你想知道哪一个给定的时间间隔重叠。 这也正是区间树是什么呢：

https://en.wikipedia.org/wiki/Interval_tree

Answer 2:

你需要一个碰撞检测算法。 在C ++中有boost.geometry用于在许多其他做这样的事情。

Answer 3:

哪里：

• 矩形是所有矩形的集合。
• R是测试矩形
• x1为一个x坐标
• X 2是其他x坐标

伪码

// make sure x1 is on the left of x2
if (R.x1 > R.x2)
    tmp = R.x2
    R.x2 = R.x1
    R.x1 = tmp
end if

for each Rect as r
    // don't test itself
    if (R != r)
        // make sure x1 is on the left of x2
        if (r.x1 > r.x2)
            tmp = r.x2
            r.x2 = r.x1
            r.x1 = tmp
        end if

        if ((r.x2 < R.x1) // if r rect to left of R rect
                || (r.x1 > R.x2)) // if r rect to right of R rect
            // r rect does not intersect R rect
        else
            // r rect does intersect R rect
        end if
    end if
end for

文章来源: Rectangles Intersection (Vertical line)