的传感器覆盖目标的最小成本的子集(Minimum cost subset of sensors co

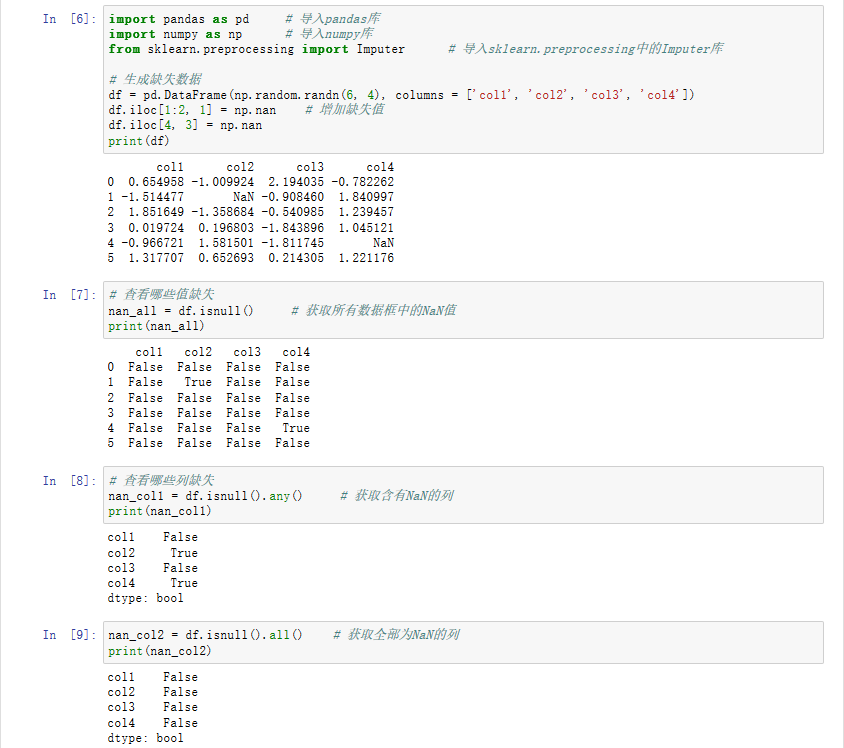
我在动态规划的一个问题，如果我有一组传感器覆盖目标（目标可能是由多发的传感器覆盖）我怎么能找到传感器知道每个传感器都有自己的成本最小的代价子集？ 我想了很多，但我不能达到递归forumla写我的程序？ 贪心算法给出我的错成本最低的子集有时，我的问题是，传感器覆盖目标重叠，任何帮助吗？

例如：我已设置传感器的成本/重量= {S1：1，S2：2.5，S3：2}和I有三个目标= {T1，T2，T3}。 传感器覆盖如下：= {S1：T1 T2，S2：T1 T2 T3，S3：T2 T3}我需要通过动态规划来获得最低的成本的子集，对于上面的例子，如果我使用贪婪算法我会得到S1，S3但正确的答案只有s2的

Answer 1:

检查第3它所标记的动态规划算法的MWCDC

https://docs.google.com/viewer?a=v&q=cache:5vPrmVg7jDMJ:www.cs.iit.edu/~wan/Journal/tcs10.pdf+&hl=en&gl=us&pid=bl&srcid=ADGEESglfvp6XtFIkqDZZ-E-Tun4AWPTZV_V7z32pTvJ05K6tdkCoefpsAxPxdK44jYDvPNLDEwYI8uK -PMlLGthsaV8-ow63utalgWPnyLrUUBKhoTTVuYwUiKSHlCXU-HXKHVeHvh4＆SIG = AHIEtbQGka8F39MaT8yAy4G9Kvv8TPsvJA

Answer 2:

我想到了什么，但我不是100％的信心吧，这里有云：

S = {s1 : 1, s2 : 2.5, s3 : 2}
M = {s1 : t1t2, s2 : t1t2t3, s3 : t2t3}

现在，我们建立代表一个矩阵target x sensor地图：

[1, 1, 0]
[1, 1, 1]
[0, 1, 1]

所以，行是目标(t1 -> R0, t2 -> R1 etc.) ，和列表示哪个传感器覆盖它们。

接下来我们处理一行接一行，同时收集将覆盖当前目标组传感器的列表。 举一个例子：

Row - 0:
{t1} -> [s1 : 1], [s2 : 2.5]

请注意，我们正在构建的答案的列表。 然后，我们进入到下一行，我们需要添加t2到我们的一系列目标，同时计算这样做所需的最小传感器的重量。

Row - 1:
{t1, t2} -> [s1 : 1], [s2 : 2.5]

需要注意的是没有任何改变的RHS因为无论s1和s2覆盖t2为好。 接下来的最后一行：

Row - 2:
{t1, t2, t3} -> [s1, s3 : 3], [s2 : 2.5]

请注意，我不得不添加s3的第一个答案，因为它有覆盖的最小重量t3 。

通过回答列表中的最后一个走就会发现， [s2 : 2.5]是最佳人选。

现在，我不与动态规划，有信心的，所以不知道我在这里做是否正确。 将是巨大的，如果有人可以证实/争什么，我在这里做。

编辑：可能是有意义的有根据传感器的权重排序的列。 从而变得易于选择具有最低权重覆盖给定的目标的传感器。

Answer 3:

这里是我的建议，这不是一个动态编程，但我可以想出，问题是有趣的，值得讨论的最好的。

---

定义“部分解决”是元组(T,S,P,C)其中T覆盖目标， S包括传感器， P是一组未决的目标， C是成本。

W是当前工作组部分的解决方案，最初仅包含({}, {}, X, 0)即成本为零，非空只是组待决的目标。 W可以维持作为堆。

W = { ({}, {}, X, 0) }
repeat
  p = select and remove from W the partial solution with the minimum cost
  if p.P is empty
     return p
  t = select from p.P the target, covered by the minimum number of sensors
  for each sensor s, covering t, which is not in p'.S
     p' = new partial solution, copy of p;
     p'.S += {s};
     p'.C += cost(s);
     for each target t' covered by s
       p'.T += {t};
       p'.P -= {t};
     end for
     W += {p'}
  end for
end repeat

Answer 4:

这是我对这个问题的算法。 它针对该问题的递归方法。

伪代码：

MinimizeCost(int cost , List targetsReached, List sensorsUsed, int current_sensor) {

if(targetsReached.count == no_of_targets ) {
    if(cost < mincost ) {
          mincost = cost;
          minList = sensorsUsed;
            }       
    return;
    }

   if(current_sensor > maxsensors)
         return;
   else {
         // Current Sensor is to be ignored 
     MinimizeCost(cost , targetsReached, sensorsUsed, current_sensor +1 );

         // Current Sensor is Considered 
     int newcost = cost + sensor_cost[current_sensor];  
     sensorsUsed.Add(current_sensor);
     AddIfNotExists(targetsReached, targets[current_sensor]);
     MinimizeCost(newcost, targetsReached, sensorsUsed, current_sensor+1);
  }
}

如果不需要这些细节可避免Sensors_Used列表。

此外记忆化可被引入到本如果TargetsReached列表可以被映射到一个int。 然后[Current_Sensor，TargetsReached]值可以保存并在需要时，为了避免重复使用。 希望这可以帮助。 虽然有可能是更好的方法。

文章来源: Minimum cost subset of sensors covering targets