转自 丛末 AI科技评论

作者 | 丛末
编辑 | 唐里
徐宗本院士在数学与 AI 之间进行了一次超强的“迁移学习”。
9 月 21 日至 22 日,为期两天的 CCAI 2019 正在秋意浓浓的中国青岛胶州隆重举行。本次会议选址室外体育馆召开,为原本严肃的学术会议增添了几分活泼、惬意的色彩。
会议第二日,徐宗本院士作为首位演讲嘉宾,从他的数学专业出发,慷慨激昂地为大家带来了主题为《AI 与数学:融通共进》的报告。
在开场前,他先从徐匡迪之问——「人工智能的基石在数学,我们有多少数学家投身进去了?」以及任正非答记者问时强调「人工智能的本质就是数学」的观点引入,表达了自己对于人工智能与数学之间的关系的看法:融通共进,一方面,人工智能的基础之一是数学,因此人工智能想要行稳致远,就必须先把数学的基本问题解决好;另一方面,人工智能的发展也对数学领域的研究产生了重要的推动作用。

在本次报告中,徐宗本院士重点分享的内容包括四个部分:第一,为理解人工智能和数学之间的关系提供一个框架,阐述数学方法与人工智能方法在处理问题的方法论上存在着本质上的一致性,因而二者能够「融通」;第二,从数学维度指出人工智能在目前发展中所存在的几个关键问题;第三,展示人工智能为数学研究所带来的新的方法论;第四,为人工智能与数学的融合方式提出具体方法。
与此同时,徐宗本院士也指出,本次他演讲中提到的「人工智能」,主要是指机器学习,虽然这只是人工智能的一部分,但是就他看来,是最能够直接成为生产力并且也是非常重要的部分。
AI 与数学:方法论上具有一致性
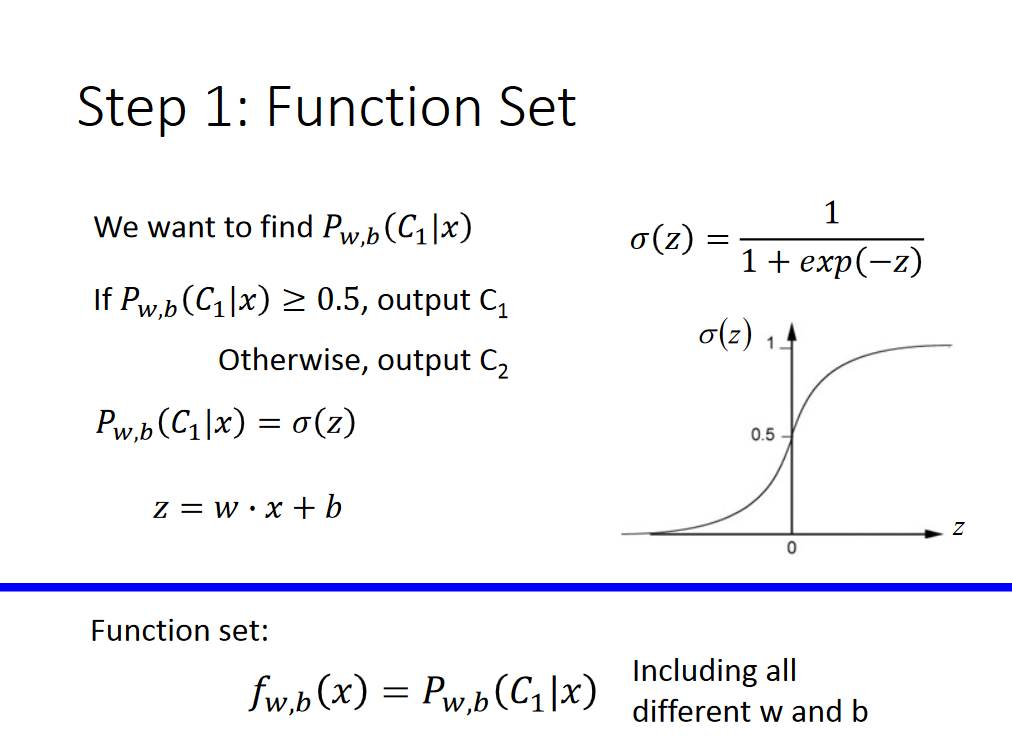
一开始,徐宗本院士对机器学习的基本概念进行了解释,他表示,简单而言,智能就是模拟人的一种行为或者说能力,即在给定环境中,能通过与环境的交互和自行来提高自身解决问题的能力,而采用一个机器或者软件来模拟这种智能时,就是机器学习。从数学的维度而言,机器学习表示的是一个函数空间或参数空间的优化问题。

他认为,无论是从机器学习还是数学,二者在解决问题上都可以用上图中的这一框架来描述,其中包括两个最为重要的部分:一个是智能体,一个是环境。
- 智能体:它是指一个含参数、可调节的任务求解器,其形态可以是深度网络,也可以是机器人、无人系统或者一个算法。
- 环境:这里所说的环境一定有两个基本性质:第一,环境是可以描述的,如果用数据来描述就是人工智能方法,如果用模型来描述就是数学方法或物理方法,如果是用知识来描述的就可能是知识工程方法等等;第二,环境是可以对其进行建模的,能够借以对智能体的行为作出判断,即可作为修正智能体行为的指标。
「具备这两个基本性质的环境加上智能体,组成的统一体便叫做机器学习系统,这其实就是我们研究问题的基本方法论。」
接下来,徐宗本院士也介绍了机器学习的几个典型模型,包括:
第一,深度学习。所谓的深度学习就是指输入一个数据,然后得到一个依赖于数据的预测或者是判断,它的环境是有标签的大数据,同时其应用的基本前提是有原因或结果组成且量很大的有序对。

第二,自编码器。当下这一代的人工智能就在于特征表述,这就涉及到自编码器这项重要的技术。编码器的任务就是提取数据的内涵特征,可以用来实现降维等任务。它的环境是无标签的数据。

第三,对抗生成(GAN)。大数据不够是大数据领域的常见问题,而对抗生成便是使用网络生成一些数据的模型。它的环境是没有标签同时量也很小的小数据,不过这些数据都是比较准确的,也就是我们所说的原数据。

第四,强化学习。强化学习时该研究领域常用的模型,它要解决的是需要对最终的决策负责的场景,比如智能驾驶需要在当下时刻知道下一步怎么走,比如说在下棋的时候也要知道走了这一步后,将对将来的胜负产生多大的影响等等。它的环境不一定是数据,比如说自动驾驶的环境就是各种传感器对身处环境的描述。

「那在这些模型中,数学和物理充当什么作用呢?以上图强化学习为例,智能体就正在解决一个数学问题,此刻它的环境就是给定的数学公式、定解条件或边界条件等。因此从本质上来看,人工智能、知识工程以及数学在解决问题时所使用的基本方法论其实是具有统一性的。」
目前,人工智能已经经过了「从一个不可用的技术发展到一个可应用的技术」的拐点,其原因有三:一是有了大量有标签的大数据;二是出现了像深度学习这样的标准模型和算法;三是拥有了强大的计算力,例如超算和云计算。

对此,徐宗本院士指出,在欣喜人工智能变成可用技术的同时,我们必须冷静地看到,目前我们距离人工智能的真正产业化,真正能把人工智能技术用得明白、也用得好,仍然还有很长一段路要走。以机器学习为例,从数据层面上讲,我们还需要使用大量的人工去标注,去选择样本;从应用层面而言,还需要自己去搭建不同的神经结构,去选择不同的训练算法,因而在现阶段,我们还处于一个「用多少人工换来多少智能」的人工智能阶段。
而要想从「可以用」走到「很好用」则还存在很多技术挑战:首先在数据样本层面上,数据样本需要实现自生成、自选择;其次在模型算法层面上,模型算法需要实现自构建、自设计;最后在环境任务层面上,环境任务要实现自适应、自转换。
「我们将实现了以上三个方面的六个特征的人工智能叫做机器学习自动化,这是我带领的研究小组这几年在主攻的方向。关于大家问到人工智能未来的发展方向,我们不妨以实现共产主义来做类比:我认为人工智能的共产主义目标是自主智能,然而在实现共产主义之前我们必须先走过社会主义初级阶段——机器学习自动化便是社会主义初级阶段目标。所以说,人工智能的发展轨迹应该是从人工走向自动化,再迈向自主智能。」
AI 面临的五大基础数学问题
基于以上提及的下一步人工智能发展目标,徐宗本院士指出,要想真正实现机器的自动化,必须首先解决以下五个数学领域的基础问题:
第一,大数据的统计学基础。人工智能应用的基本模式则包括感、知、控三个部分,其中,感,就是将环境中的各种要素通过各种各样的传感器变成数据的数字化过程;知,就是指能读懂大数据,这是机器学习的主要部分;控,则是指机器将由数据得到的知识和规则用于实际控制。贯穿着三个基本模型的核心技术便是大数据,而统计学则是理解、分析大数据的基础。目前,支持大数据分析的数学基础尚未完全建立起来。

第二,大数据计算基础算法。大数据一般应用于分析处理两类基本任务:一类是以计算机逻辑为基础的搜索、比对、排序、溯源等问题;一类是分析数据之间是否具有共性结构等的聚类、分类、回归等问题。这两类问题都以数学模型为基础。然而一些传统的计算,在大数据环境下都变成了全新的问题,因而针对大数据环境重建大数据计算的基础算法和分析处理算法,都成为当下亟待解决的问题。

第三,深度学习的数学原理。「深度学习现在存在很多毛病,张钹院士昨天也说过了,然而深度学习是目前最能够为大家所普遍接受的人工智能技术之一,就像高考,虽然被人诟病很多,但是目前还没有更好的方式来替代它一样,深度学习同样如此。比如它存在的可解释性问题,主要还是因为它无法使用明确的数据公式来进行展开,因而如何从数学上证明深度学习在每一层网络上的展开情况,是当下迫在眉睫的事情;另外,什么样的结构决定什么样的性质,因而我们还需要研究清楚深度学习中结构和性质的关系问题。

第四,非常规约束下的输运问题。人工智能的很多问题都可以抽象为:将一个领域的数据转移到另外一个领域的数据,比如说机器翻译,就实现不同语言之间的转换问题。这自然就涉及到「什么样的数据之间能够进行转移」的问题。而众所周知,能够实现转移的前提是,两个领域之间的数据存在一「公共不变量」,这是数学的标准术语。比如说机器能翻译就存在语义这一不变量,例如医疗应用同样遵循这一思路,即 CT 图象转成核磁图象过程中,同一个人本身就是就是这个不变量。如何判断数据能够被转移,以及如何实现不同领域的数据转移问题,就叫做非传统约束下的传输问题。

第五,学习方法论的建模与函数空间上的学习理论。目前机器学习所处的阶段是:数据是中心以及机器学习和泛化的对象。这就要求数据对问题具有普适性、可推广性以及学习性,数学中对此的一个提法是学习方法论或者说函数空间上的学习理论。在迈向机器学习自动化之前,就必须使其具有对相关问题的公共方法论的学习,然而目前这还是一个全新的研究领域,暂时还没有出现相关的研究框架。

「这五个问题是通向自主智能锁必须解决的基本问题,而这也反过来说明了为什么我们都说人工智能的基石在数学的原因。」
AI 为数学提供全新视角
数学对于人工智能的基础性作用不言而喻,而反过来,人工智能技术同样也为数学领域的研究带来了全新的视角,并带来了一些革命性影响。徐宗本院士主要基于人工智能为优化、PDE 问题的数学研究所带来的推动作用,进行了该部分的介绍。
1、AI 对优化的应用

最优化是数学的基本问题,然而数学传统在研究这个问题上有很多的局限性,包括无法实现全局优化、不涉及超参数问题以及适配性问题等,例如在局部优化方面研究得很彻底,但就是没有人研究解决某个「世纪」问题应该用什么方法。而人工智能在这几个问题上的应用,都能带来非常可喜的结果。
徐宗本院士表示,人工智能对优化问题的研究带来了全新的思考,对此他提到了三个案例:
第一,解决适配性问题。「Learn to Learn」这个方法最早出现于 2006 年,随后就一发不可收拾地出现了很多技术,包括「学会搜索」、「学会 teach」、「学会推理」等以「学会」为主体的推理方法。这类方法都是从宏观学习方法论的角度解决问题,基于这些方法,现在我们已经有了一个对任意优化问题都可用的自适应优化器。

第二,解决超参数问题。以压缩感知问题为例,下图为压缩感知的基本框架。公式中,第一项是拟合项,现在采用人工智能技术以后,可以在公式中将超参数作为参数使用,对照着问题去训练,能够一次性地把压缩感知的选择问题解决,该方法尤其是在图象处理、医疗成像等应用中,都是实现了目前性能最好的神经网络模型。

第三,解全局优化问题。全局优化问题一直以来都是个难题,但如果从强化学习的视角来解决这个问题,它的面貌就会焕然一新。比如在 MNIST 手写数字识别中要解决 7960 维的优化问题,就可以使用全梯度下降方法来进行优化。

2、AI 对 PDE 问题的应用
而人工智能对 PDE 问题的应用,同样被徐宗本院士视作人工智能在数学中的成功应用。下图中公式为 PDE 的一般形式:第一行方程式是含导数的关系式;第二行方方程式则是指该函数应该满足的初始条件;第三行方程式方式则表示公式在边界情况下的对应关系。三个方程式合在一起就是微分方程定解问题。

对此,数学家已经提出了有限差分法、有限元法、有限体方法等等,都很成功,然而不得不承认的是,在解决复杂边界以及复杂的函数时,这些方法的效果并不好。而人工智能则为这一问题提供了一个全新的视角和完全不同的解决方向,即利用对空间的采样即积分方法来提到离散化的微分方法。
对应人工智能的框架来说,可以将智能体理解为找微分方程解,环境就可以理解为上面方程式给出的初始条件和边界对应关系。基于这种方法,最终能够让神经网络逼近微分方程的解。
同时,徐宗本院士还特别介绍了 AI 在反问题中的应用。他指出,反问题是 CT、核磁共振、雷达等应用的基础之基础,都是根据已知的东西推理未知的东西,而如果将这些问题改造成神经网络的话,就能带来意想不到的效果。
首先是受到编码器的启示,他对自编码器提供的「黑箱」编码、解码以及数据编码、解码的方法进行改造,提出了模型驱动、机理溶入的反问题求解框架,并由此提出解反问题的无监督学习、全监督学习和半监督学习的三种模式都采用这一框架去实现的观点。

其次在解线性方程组的应用上,此前,Y=aX 作为线性方程组的基本公式,我们一定需要知道 a 的具体值以及是否可逆的等等。而现在深度学习则能够做到「不问东西」、「不问青红皂白」地直接给出解。

另外在地震波反演的应用上,在使用人工智能方法后,地震勘探不再只是单纯解偏方程数字解,最终更能够「看清楚」地底下的情况。

AI 与数学,融通方法论
演讲最后,徐宗本院士还对 AI 与数学未来的「融合共通」发展进行了展望,提出了具体的研究方向。他指出,从认识论和方法论上来看,数学与 AI 交互作用的本质是提倡「模型驱动」与「数据驱动」的结合,而这种结合具有巨大的潜力,其中具体的结合方式包括:
第一,数据不够模型补,模型不精数据上。「这句话,这两年我说过很多次,现在我越来越觉得这两句话很对。一方面,当我们抱怨数据不够时,我们还可以想想我们在几十年的研究中已经积攒了很多模型,并且模型就是数据的升华,因而用上一个好的模型可以大大减少对数据的依赖性;另一方面,模型好自然很好,然而当无法实现一个精致的模型时,我们还能够用数据去补,实际上现在在很多科学研究中,研究者们都在用数据弥补模型上的不足。」
第二,物理机理启发,知识融入。「这同样也是极为重要的科学方法论,是我们可以用来提高解决问题的质量以及人工智能效能的重要法宝。」
(完)
更多 CCAI 2019 内容请期待后续报道。