流通网络流量(Circulation in network flow)

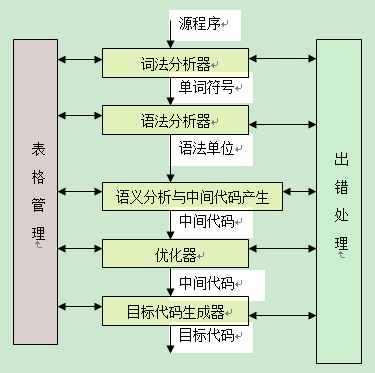
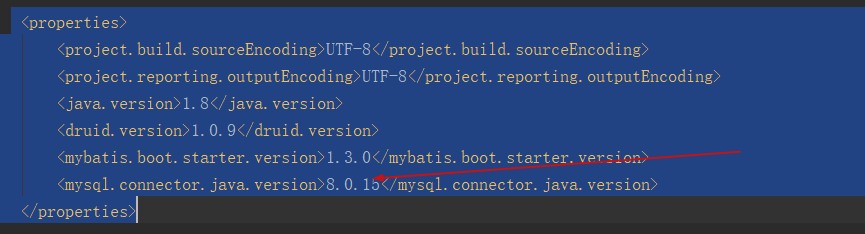
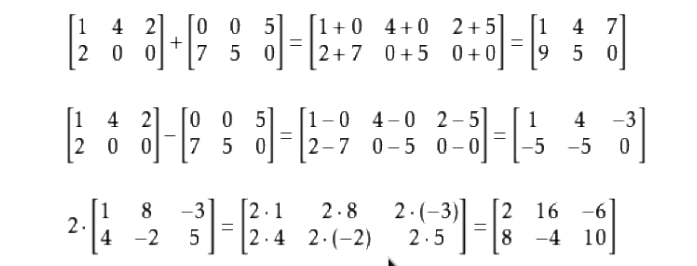我读的书的算法由罗伯特Sedwick写的。

注：“S”是源和“t”是坦克。

Augument任何流网络与来自“T”，以“s”用流和容量等于网络的值的边缘，并且知道流入等于流出的augumented网络中的任何节点集。 这种流动被称为循环，这种结构表明，maxflow问题简化为找到最大化沿着给定边流动的流通问题。

给定一组的周期和每个循环的流量值，很容易通过每个循环之后，加入所指示的流向每个边缘以计算相应的循环。 相反的属性是更令人惊讶的; 我们可以找到一组循环（对每个流量值），其等效于任何给定的循环。

流分解表示定理：任何循环可以被表示为沿着一组atmostË定向循环流动。

我上面的解释问题

1. 请用例子来解释这是什么意思的作者，以及我们如何能减少“maxflow问题简化为找到最大化沿着一个给定边流循环的问题。”？

2. 任何一个可以与下面的一段简单的例子说明。

“给定一组的周期和每个循环的流量值，很容易通过每个循环之后，加入所指示的流给每个边缘，以计算相应的循环反过来属性是更令人惊奇的;我们可以找到一组循环（对于每个流动值），其等效于任何给定的循环“。

谢谢！

Answer 1:

1. 如果你有源S和汇吨maxflow问题，您可以只需添加一个边缘的T> s此问题转化为最大的流通问题。 从s至t原有最大流现在转换成最大循环小号---> T->秒。

2. 如果您有周期的列表（在图形中的封闭路径），每个周期与流动氮相关的，你可以通过所有的循环，并添加流量值N到那些边缘周期经历。 以这种方式，在图形中的每条边都会有它计算的流量值，这是图表中的总发行量。 相反，该定理说，只要你有在总图的循环，它可以分解为周期。 这里是一个最大循环的一个例子，在每个边缘上的符号A（B）表示该流是与边缘的最大容量为b：

     3(3) 2(2) a ----> b -----> c ^ |1(1) | |3(3) VV 2(4) d<------e<-------f 3(4) 2(3) 

相应的周期是：abeda与流量值1，并用流量值2. abcfed这两个周期一起限定的最大循环，如上所示。

文章来源: Circulation in network flow