Convolution of two fft function

问题:

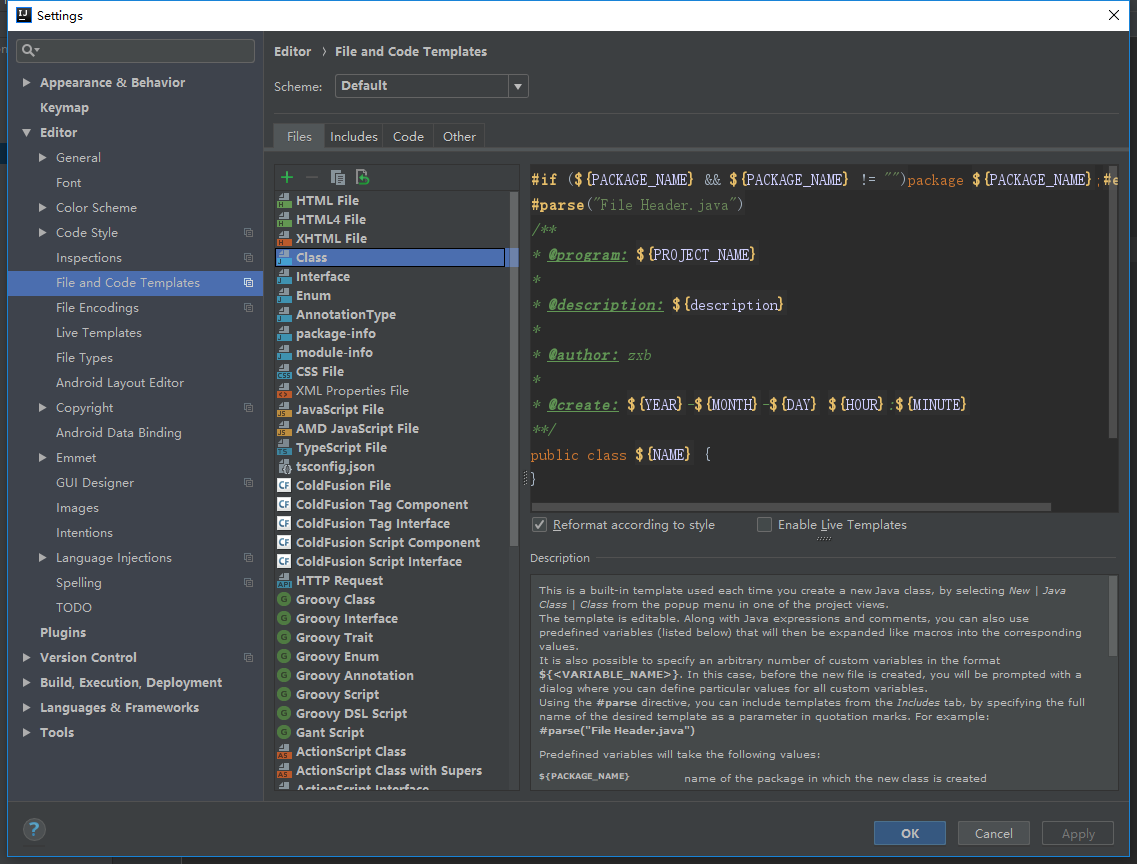
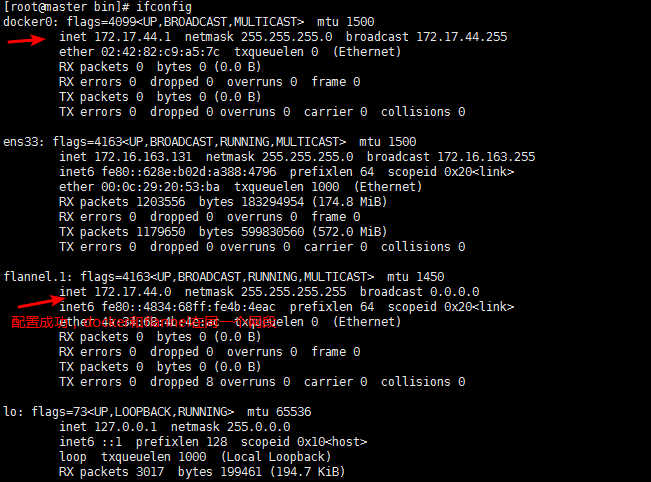
For convolution theorem F(x.y) = F(x)*F(y)

However after implement it on python

x = np.array([0,0,0,0,1, 2, 3, 4, 0 ,0,0,0])
y = np.array([0,0,0,0,-3, 5, -4, 0, 0, 0,0,0])

xy = x*y
inverse_fft_xy = np.fft.ifft(np.convolve(np.fft.fft(x),np.fft.fft(y)))

Will yield

xy

array([  0,   0,   0,   0,  -3,  10, -12,   0,   0,   0,   0,   0])

inverse_fft_xy

array([  0.00000000e+00,  -8.70383905e-01,   1.65925305e-02,
    -8.90888514e-01,   7.07822398e-02,  -8.80447879e-01,
     1.19687210e-01,   3.09247006e+00,  -9.54481834e+00,
    -5.81203213e+00,   2.15726342e+01,  -1.47366137e+01,
    -1.03012447e+01,   2.76823117e+00,  -1.42560168e+00,
     4.98000293e-01,  -1.18537317e+00,   2.02675981e-01,
    -9.98770784e-01,   7.43392335e-02,  -9.11516399e-01,
     1.67799168e-02,  -8.74501632e-01])

and it is the same for matlab

I know that there should be zeros padded to avoid linear convolution. Also, the other way of theorem F(x*y) = F(x).F(y) can be done. I just want to know why it cannot be done this way.

回答1:

The time-domain multiplication is actually in terms of a circular convolution in the frequency domain, as given on wikipedia:

Following @Ami tavory's trick to compute the circular convolution, you could implement this using:

Xf = np.fft.fft(x)
Yf = np.fft.fft(y)
N = Xf.size    # or Yf.size since they must have the same size
conv = np.convolve(Xf, np.concatenate((Yf,Yf)))
conv = conv[N:2*N]
inverse_fft_xy = np.fft.ifft(conv) / N

such that

x = np.array([1, 2, 3, 4])
y = np.array([-3, 5, -4, 0])

(without any more zero padding than is necessary to have both arrays the same size) would yield the expected:

xy

array([  -3,  10, -12,   0  ])

inverse_fft_xy

array([ -3.+0.j, 10.+0.j, -12.+0.j, 0.+0.j])