产生一定等级的“随机”基质上固定的一组元素(Generate “random” matrix of

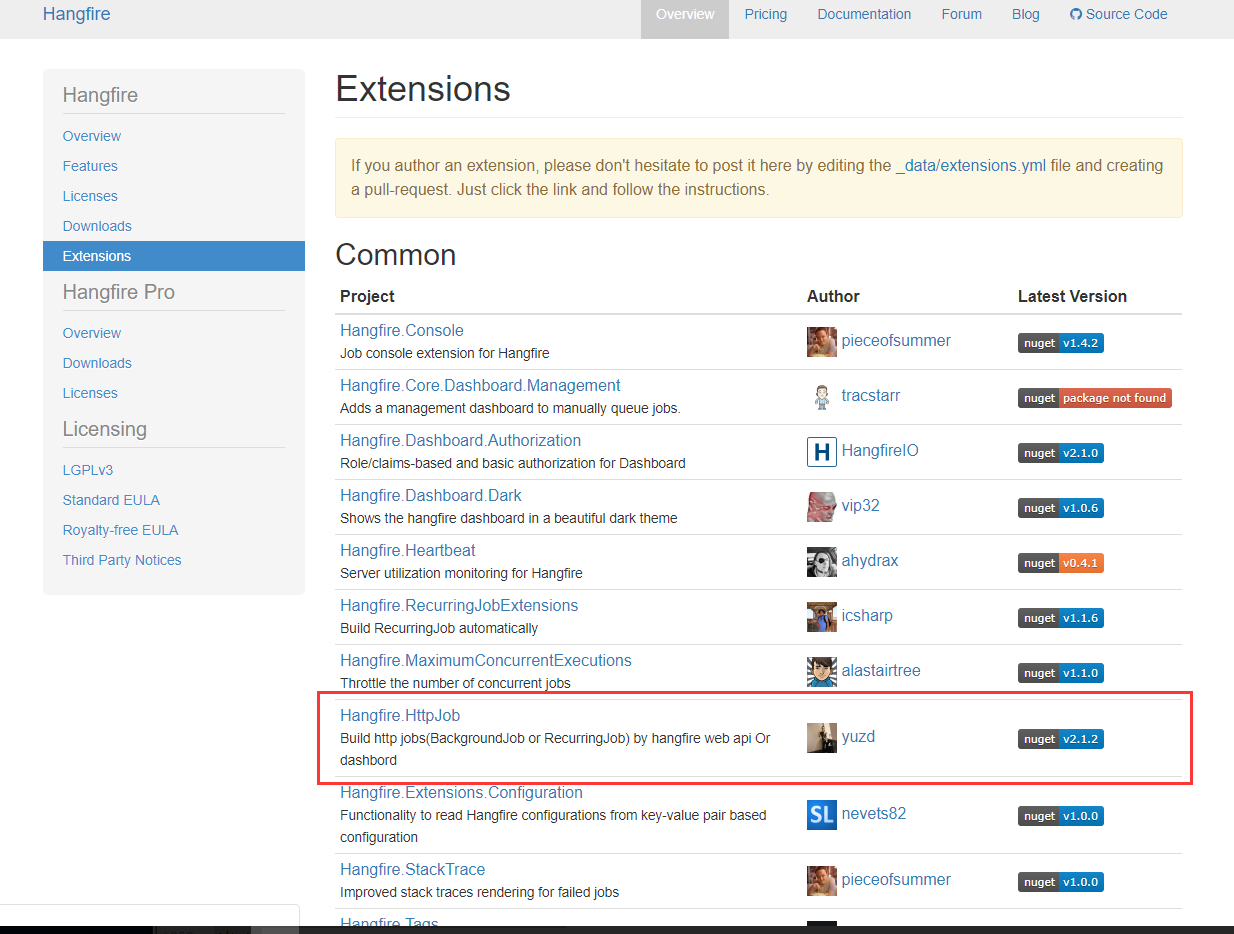
我想生成大小的矩阵m X n和秩r包含元素从指定的有限集合，例如未来{0,1}或{1,2,3,4,5} 我希望他们能在这个词的一些很不确切的“随机”，即我想从与分布依稀相似，所有矩阵超过该集合与指定等级元素的分布算法获得各种可能的输出。

其实，我并不真正关心它的秩r只是它的接近秩的矩阵r由弗罗比尼斯范数计）。

当设置在手是实数，我已经执行以下操作，这是完全足够我需要：生成矩阵U尺寸的m X r和V的n X r ，0从例如普通独立地采样元件（， 2）。 然后U V'是一个m X n秩的矩阵r当然， <= r ，但我认为这是r以高概率）。

如果我这样做，然后一轮二进制/ 1-5，不过，排名上升。

它也可以通过做SVD和采取率先拿到下级近似矩阵r奇异值。 这些值，不过，不会说谎在所需的设定，并四舍五入他们将再次提高等级。

这个问题是相关的，但接受的答案是没有“随机”而对方的回答表明，SVD，这是指出不会在这里工作。

我想过的一种可能性是，使r从组线性无关的行或列向量，然后通过这些的线性组合获得其矩阵的其余部分。 我不是很清楚，不过，无论是如何获得“随机”线性无关向量，或者如何在他们之后，一个准随机的方式结合起来。

（不，它是超相关的，但我在numpy的事情了。）

---

更新：我已经试过在评论由EMS建议的方法，用这种简单的实现：

real = np.dot(np.random.normal(0, 1, (10, 3)), np.random.normal(0, 1, (3, 10)))
bin = (real > .5).astype(int)
rank = np.linalg.matrix_rank(bin)
niter = 0

while rank > des_rank:
    cand_changes = np.zeros((21, 5))
    for n in range(20):
        i, j = random.randrange(5), random.randrange(5)
        v = 1 - bin[i,j]
        x = bin.copy()
        x[i, j] = v
        x_rank = np.linalg.matrix_rank(x)
        cand_changes[n,:] = (i, j, v, x_rank, max((rank + 1e-4) - x_rank, 0))
    cand_changes[-1,:] = (0, 0, bin[0,0], rank, 1e-4)

    cdf = np.cumsum(cand_changes[:,-1])
    cdf /= cdf[-1]
    i, j, v, rank, score = cand_changes[np.searchsorted(cdf, random.random()), :]
    bin[i, j] = v
    niter += 1
    if niter % 1000 == 0:
        print(niter, rank)

它的工作原理迅速为小矩阵，但分崩离析为10×10如 - 它似乎停留在6级或7点，至少重复成千上万。

看起来这可能工作有一个更好的（即不太平坦的）目标函数更好，但我不知道这是什么会。

---

我也尝试了建立矩阵简单的消除方法：

def fill_matrix(m, n, r, vals):
    assert m >= r and n >= r
    trans = False
    if m > n: # more columns than rows I think is better
        m, n = n, m
        trans = True

    get_vec = lambda: np.array([random.choice(vals) for i in range(n)])

    vecs = []
    n_rejects = 0

    # fill in r linearly independent rows
    while len(vecs) < r:
        v = get_vec()
        if np.linalg.matrix_rank(np.vstack(vecs + [v])) > len(vecs):
            vecs.append(v)
        else:
            n_rejects += 1
    print("have {} independent ({} rejects)".format(r, n_rejects))

    # fill in the rest of the dependent rows
    while len(vecs) < m:
        v = get_vec()
        if np.linalg.matrix_rank(np.vstack(vecs + [v])) > len(vecs):
            n_rejects += 1
            if n_rejects % 1000 == 0:
                print(n_rejects)
        else:
            vecs.append(v)
    print("done ({} total rejects)".format(n_rejects))

    m = np.vstack(vecs)
    return m.T if trans else m

这工作好与任何级别如10×10的二值矩阵，而不是0-4矩阵或更低级别更大的二进制文件。 （例如，获取等级15的20×20二元矩阵把我拒绝42000;与排名10的20×20，花了120万美元。）

这显然是因为由第一跨越的空间r行是我是从取样的空间中，例如过小的部分{0,1}^10 ，在这些情况下。

我们希望第一跨度的交叉r行与有效值的集合。 因此，我们可以尝试从跨度采样，并寻找有效的值，但由于跨度涉及这永远不会找到我们有效载体实值系数（即使我们正常化使得例如第一部分是在有效集）。

也许这可以用公式为整数规划问题，还是什么？

Answer 1:

我的朋友，丹尼尔·约翰逊谁上述评论，想出了一个主意，但我看到他从来没有张贴。 它不是很充实手续，但你也许能够适应它。

如果A是m乘r和B为r乘n并且两者都具有秩r然后AB具有秩r。 现在，我们只需要挑A和B ，使得AB只能在给定的有值。 最简单的例子是S = {0,1,2,...,j}

一个选择是使A与相应的行/列总和二进制即保证正确的秩和B与列总和增加至不超过j （使得产品中的每个项是S ）和行总和拾取引起秩r （或者至少鼓励它作为排斥反应可以使用）。

我只是认为我们能拿出两个独立的采样方案A和B是那么复杂，不是试图在一次攻击整个矩阵更快。 不幸的是，我所有的基质取样代码是在其他计算机上。 我知道它在一组比大容易推广到允许条目{0,1}即S ），但我不记得如何计算与缩放m*n 。

Answer 2:

这个怎么样？

rank = 30
n1 = 100; n2 = 100
from sklearn.decomposition import NMF
model = NMF(n_components=rank, init='random', random_state=0)
U = model.fit_transform(np.random.randint(1, 5, size=(n1, n2)))
V = model.components_
M = np.around(U) @ np.around(V)

Answer 3:

我不知道这个解决方案会多么有用，但你可以构建一个矩阵，让你寻找另一矩阵解决方案，只有0和1的条目。 如果您对二元矩阵随机搜索，它相当于随机修改最终矩阵的元素，但也可以拿出一些规则做多随机搜索更好。

如果要产生一个m -by- n以上的元素集合E的元件矩阵E _I， 0<=i<k则与开始m -by- k*m矩阵，A：

显然，这种矩阵具有秩米 。 现在，您可以构建另一个矩阵，B，有在某些位置1S挑选从集合E的元素。 该矩阵的结构是：

每个B _i是k -by- n矩阵。 所以，A B的大小为m -by- n和秩（A B）是min（米，秩（B））。 如果我们要输出矩阵，从我们的集合，E，那么每个B的专栏中， _我必须有一个元素设置为仅要素1 ，其余设置为0 。

如果你想搜索基于B一定的等级随机，你需要用最高等级的有效b启动了，并通过随机量旋转_我随机B的随机j列。 这相当于改变专栏中， 我行A * B j的从我们设定一个随机元素，所以它不是一个非常有用的方法。

但是，你可以用矩阵一定的技巧。 例如，如果k是2，并且对B _0，和B ₁的第一行没有重叠，则可以通过将这些两个子矩阵的第一行产生线性相关的行。 第二行也将是线性地依赖于这两个矩阵的行。 我不知道这是否会很容易地推广到k大于2，但我相信会有你可以使用其他的技巧。

例如，一种简单的方法，以产生至多秩k （当m为k+1 ）是获得一个随机有效_B0，不断旋转该矩阵的所有行到获得乙₁至B _M-2，设置第一排的B _M-1至全为1，而其余的行的所有0秩不能小于k （假设n > k ），因为B_0列具有恰好1非零元素。 矩阵的剩余行都是线性组合（在几乎所有的子矩阵事实精确副本）这些行的。 最后一个子矩阵的第一行是第一子矩阵的所有行的总和，它的其余行都是零。 对于较大的值m ，可以使用乙_0，而不是简单的旋转的行的排列。

一旦你生成满足秩约束一个矩阵，你可以逃脱随机洗牌的行和列其生成等。

文章来源: Generate “random” matrix of certain rank over a fixed set of elements