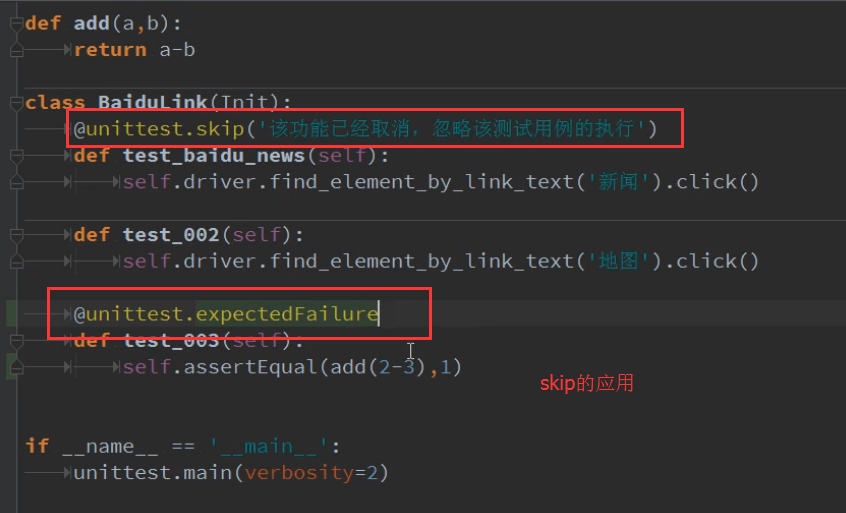
我有在空间,例如两个点的min的向量:
A = np.array([-1452.18133319 3285.44737438 -7075.49516676])
B = np.array([-1452.20175668 3285.29632734 -7075.49110863])
我想找到载体的切线沿曲线离散点,GG曲线的开始和结束。 我知道如何做到这一点在Matlab,但我想这样做在Python。 这是在Matlab代码:
A = [-1452.18133319 3285.44737438 -7075.49516676];
B = [-1452.20175668 3285.29632734 -7075.49110863];
points = [A; B];
distance = [0.; 0.1667];
pp = interp1(distance, points,'pchip','pp');
[breaks,coefs,l,k,d] = unmkpp(pp);
dpp = mkpp(breaks,repmat(k-1:-1:1,d*l,1).*coefs(:,1:k-1),d);
ntangent=zeros(length(distance),3);
for j=1:length(distance)
ntangent(j,:) = ppval(dpp, distance(j));
end
%The solution would be at beginning and end:
%ntangent =
% -0.1225 -0.9061 0.0243
% -0.1225 -0.9061 0.0243
有任何想法吗? 我试图找到使用numpy的解决方案,并SciPy的使用多种方法,如
tck, u= scipy.interpolate.splprep(data)
但没有一种方法似乎满足我想要的东西。
给der=1至splev拿到样条曲线的导数:
from scipy import interpolate
import numpy as np
t=np.linspace(0,1,200)
x=np.cos(5*t)
y=np.sin(7*t)
tck, u = interpolate.splprep([x,y])
ti = np.linspace(0, 1, 200)
dxdt, dydt = interpolate.splev(ti,tck,der=1)
确定,我发现该溶液是上述的“PV”稍加修改(注意splev仅适用于一维向量)我用“TCK,U = scipy.interpolate.splprep(数据)”原本具有的一个问题是,它需要4个点分上班(Matlab的工作连得两分)。 我用的是两分。 增加数据点之后,它的工作原理是我想要的。
下面是完整的解决方案:
import numpy as np
import matplotlib.pyplot as plt
from scipy import interpolate
data = np.array([[-1452.18133319 , 3285.44737438, -7075.49516676],
[-1452.20175668 , 3285.29632734, -7075.49110863],
[-1452.32645025 , 3284.37412457, -7075.46633213],
[-1452.38226151 , 3283.96135828, -7075.45524248]])
distance=np.array([0., 0.15247556, 1.0834, 1.50007])
data = data.T
tck,u = interpolate.splprep(data, u=distance, s=0)
yderv = interpolate.splev(u,tck,der=1)
和所述切线(其Matlab的结果相匹配,如果使用相同的数据):
(-0.13394599723751408, -0.99063114953803189, 0.026614957159932656)
(-0.13394598523149195, -0.99063115868512985, 0.026614950816003666)
(-0.13394595055068903, -0.99063117647357712, 0.026614941718878599)
(-0.13394595652952143, -0.9906311632471152, 0.026614954146007865)