How to output all possible combinations using loop

问题:

I just started to learn programming and am trying to write a function that outputs all possible combinations. So far I've been able to find all possible combinations of size 2 but I'm not sure how to leave the code open ended to deal with combinations of larger sizes. Would some sort of recursion would be useful?

I know I could use the built in combination method but I'm just trying to figure out how to write it from scratch. Any advice would be much appreciated. Thanks!

def two_combos(input)
    list = []
    for index1 in (0...input.length)
        for index2 in (0...input.length)
            if input[index1] != input[index2]
                if list.include?([input[index2],input[index1]])==false
                    list << [input[index1],input[index2]]
                end
            end
        end
    end
    return list
end


two_combos(["A","B","C"])
#outputs
=> [["A", "B"], ["A", "C"], ["B", "C"]]
#Missing
["A","B","C"]

回答1:

This implementation is like counting recursively in binary:

def combinations(items)
  return [] unless items.any?
  prefix = items[0]
  suffixes = combinations(items[1..-1])
  [[prefix]] + suffixes + suffixes.map {|item| [prefix] + item }
end

> combinations(%w(a b c))
=> [["a"], ["b"], ["c"], ["b", "c"], ["a", "b"], ["a", "c"], ["a", "b", "c"]]

At each stage, the combinations are a concatenation of:

• the first element alone
• the combinations of the following elements (elements 1..n-1)
• the first element combined with the combinations of the following elements

回答2:

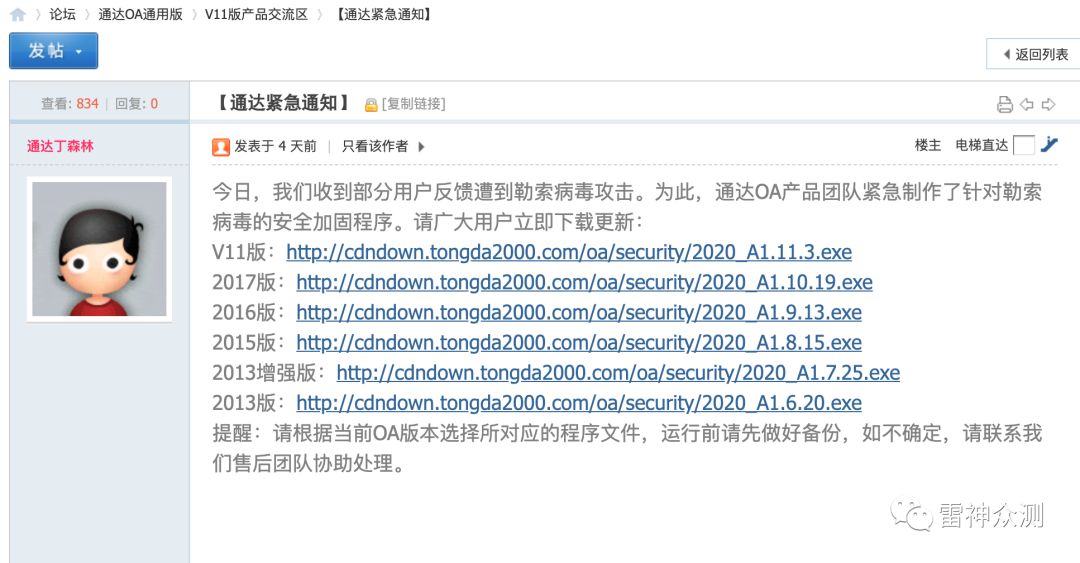
Here is recursive algorithm

def combinations(array, size)
  fail "size is too big" if size > array.size

  combination([], [], array, size)
end

def combination(result, step, array, size)
  steps = size - step.size
  array[0..-steps].each_with_index do |a, i|
    next_step = step + [a]
    if next_step.size < size
      combination(result, next_step, array[i+1..-1], size)
    else
      result << next_step
    end
  end
  result
end

a = ("A".."E").to_a
p combinations(a, 1)
# [["A"], ["B"], ["C"], ["D"], ["E"]]
p combinations(a, 2)
# [["A", "B"], ["A", "C"], ["A", "D"], ["A", "E"], ["B", "C"], ["B", "D"], ["B", "E"], ["C", "D"], ["C", "E"], ["D", "E"]]
p combinations(a, 3)
# [["A", "B", "C"], ["A", "B", "D"], ["A", "B", "E"], ["A", "C", "D"], ["A", "C", "E"], ["A", "D", "E"], ["B", "C", "D"], ["B", "C", "E"], ["B", "D", "E"], ["C", "D", "E"]]
p combinations(a, 4)
# [["A", "B", "C", "D"], ["A", "B", "C", "E"], ["A", "B", "D", "E"], ["A", "C", "D", "E"], ["B", "C", "D", "E"]]

回答3:

I can think of a way to calculate combinations of a given size without using recursion, but it is not especially efficient. It is very efficient, however, if you want to obtain all combinations of all sizes (sometimes referred to as "power"). [Edit: evidently not. See the benchmark.] My understand is that the question concerns the latter, but I will give methods for each.

If index has n elements, each combination can be represented by an n-element array whose elements are each zero or one, 1 meaning the combination includes the element at that index, '0' (or a leading space) meaning it does not. We therefore can generate the set of all combinations of all sizes by simply generating all binary numbers of length n, converting each from its string representatation (with leading zeroes) to an array of "0"'s and "1"s, replacing the "1"'s with their index positions, removing the "0"'s and extracting the element of index at the given index positions.

Code

def all_combos(sz)
  [*(0..2**sz-1)].map { |i| ("%0#{sz}b" % i).chars }
                 .map { |a| a.each_with_index
                             .select { |n,ndx| n=="1" }.map(&:last) }
end

def combos(input, n, all_combos)
  all_combos.select { |c| c.size == n }.map { |c| input.values_at(*c) }
end

def power(input, all_combos)
  all_combos.map { |c| input.values_at(*c) }
end

Example

input = %w{b e a r s}
   #=> ["b", "e", "a", "r", "s"]
ac = all_combos(input.size)
  #=> [[], [4], [3], [3, 4], [2], [2, 4], [2, 3], [2, 3, 4],
  #    [1], [1, 4], [1, 3], [1, 3, 4], [1, 2], [1, 2, 4], [1, 2, 3],
  #    [1, 2, 3, 4], [0], [0, 4], [0, 3], [0, 3, 4], [0, 2], [0, 2, 4],
  #    [0, 2, 3], [0, 2, 3, 4], [0, 1], [0, 1, 4], [0, 1, 3], [0, 1, 3, 4],
  #    [0, 1, 2], [0, 1, 2, 4], [0, 1, 2, 3], [0, 1, 2, 3, 4]]

(0..input.size).each { |i| puts "size #{i}"; p combos(input, i, ac) }
  # size 0
  # [[]]
  # size 1
  # [["s"], ["r"], ["a"], ["e"], ["b"]]
  # size 2
  # [["r", "s"], ["a", "s"], ["a", "r"], ["e", "s"], ["e", "r"],
  #    ["e", "a"], ["b", "s"], ["b", "r"], ["b", "a"], ["b", "e"]]
  # size 3
  # [["a", "r", "s"], ["e", "r", "s"], ["e", "a", "s"], ["e", "a", "r"],
  #    ["b", "r", "s"], ["b", "a", "s"], ["b", "a", "r"], ["b", "e", "s"],
  #    ["b", "e", "r"], ["b", "e", "a"]]
  # size 4
  # [["e", "a", "r", "s"], ["b", "a", "r", "s"], ["b", "e", "r", "s"], 
  #    ["b", "e", "a", "s"], ["b", "e", "a", "r"]]
  # size 5
  # [["b", "e", "a", "r", "s"]]

power(input, ac)
  #=> [[], ["s"], ["r"], ["r", "s"], ["a"], ["a", "s"], ["a", "r"],
  #    ["a", "r", "s"], ["e"], ["e", "s"], ["e", "r"], ["e", "r", "s"],
  #    ["e", "a"], ["e", "a", "s"], ["e", "a", "r"], ["e", "a", "r", "s"],
  #    ["b"], ["b", "s"], ["b", "r"], ["b", "r", "s"], ["b", "a"],
  #    ["b", "a", "s"], ["b", "a", "r"], ["b", "a", "r", "s"], ["b", "e"],
  #    ["b", "e", "s"], ["b", "e", "r"], ["b", "e", "r", "s"], ["b", "e", "a"],
  #    ["b", "e", "a", "s"], ["b", "e", "a", "r"], ["b", "e", "a", "r", "s"]]

回答4:

Gentlemen, start your engines!

Methods compared

module Methods
  def ruby(array)
    (0..array.size).each_with_object([]) { |i,a|
       a.concat(array.combination(i).to_a) }
  end

  def todd(input)
    permutations(input) << []
  end

  private

  def permutations(items)
    return [] unless items.any?
    prefix = items[0]
    suffixes = permutations(items[1..-1])
    [[prefix]] + suffixes + suffixes.map {|item| [prefix, item].flatten }
  end

  public

  def fl00r(array)
    (1..array.size).each_with_object([]) { |i,a|
       a.concat(combinations(array, i)) } << []
  end

  private

  def combinations(array, size)
    fail "size is too big" if size > array.size
    combination([], [], array, size)
  end

  def combination(result, step, array, size)
    steps = size - step.size
    array[0..-steps].each_with_index do |a, i|
      next_step = step + [a]
      if next_step.size < size
        combination(result, next_step, array[i+1..-1], size)
      else
        result << next_step
      end
    end
    result
  end

  public

  def cary(input)
    ac = all_combos(input.size)
    ac.map { |c| input.values_at(*c) }
  end

  private

  def all_combos(sz)
    [*0..2**sz-1].map { |i| ("%0#{sz}b" % i).chars }
                 .map { |a| a.each_with_index.select { |n,ndx| n=="1" }.map(&:last) }
  end
end

Test data

def test_array(n)
  [*1..n]
end

Helpers

def compute(arr, meth)
  send(meth, arr)
end  

def compute_sort(arr, meth)
  compute(arr, meth).map(&:sort).sort
end

Include module

include Methods
@methods = Methods.public_instance_methods(false)
  #=> [:ruby, :todd, :fl00r, :cary]

Confirm methods return the same values

arr = test_array(8)

a = compute_sort(arr, @methods.first) 
puts @methods[1..-1].all? { |m| a == compute_sort(arr, m) }
  #=> true

Benchmark code

require 'benchmark'

@indent = methods.map { |m| m.to_s.size }.max

[10, 15, 20].each do |n|
  puts "\nn = #{n}"
  arr = test_array(n)
  Benchmark.bm(@indent) do |bm|
    @methods.each do |m|
      bm.report m.to_s do
        compute(arr, m).size
      end
    end
  end
end

Tests (seconds)

n = 10
                                 user     system      total        real
ruby                         0.000000   0.000000   0.000000 (  0.000312)
todd                         0.000000   0.000000   0.000000 (  0.001611)
fl00r                        0.000000   0.000000   0.000000 (  0.002675)
cary                         0.010000   0.000000   0.010000 (  0.010026)

n = 15
                                 user     system      total        real
ruby                         0.010000   0.000000   0.010000 (  0.010742)
todd                         0.070000   0.010000   0.080000 (  0.081821)
fl00r                        0.080000   0.000000   0.080000 (  0.076030)
cary                         0.430000   0.020000   0.450000 (  0.450382)

n = 20
                                 user     system      total        real
ruby                         0.310000   0.040000   0.350000 (  0.350484)
todd                         2.360000   0.130000   2.490000 (  2.487493)
fl00r                        2.320000   0.090000   2.410000 (  2.405377)
cary                        21.420000   0.620000  22.040000 ( 22.053303)

I draw only one definitive conclusion.